Módulo 2

Técnicas de Amostragem

A estatística é uma ferramenta poderosa que nos permite compreender o mundo ao nosso redor por meio da análise de dados. No entanto, muitas vezes é impossível ou impraticável coletar informações sobre uma população inteira. É aí que entram as técnicas de amostragem, um conjunto de métodos que nos permitem extrair informações significativas de uma pequena porção da população para fazer inferências precisas sobre o todo.

Neste tópico, vamos explorar diferentes métodos de amostragem que nos ajudarão a escolher amostras de forma aleatória, sistemática e estratégica. Aprenderemos como calcular o tamanho adequado da amostra para atingir nossos objetivos de pesquisa e minimizar os erros de amostragem.

Vantagens na realização de amostragem:

Redução de custos, é mais barato entrevistar algumas centenas de pessoas do que milhares de pessoas

Maior rapidez, é mais rápido obter informações de centenas de unidades amostrais do que milhares de unidades

Maior amplitude e flexibilidade, é mais fácil organizar os trabalhos para observar parte da população.

Maior exatidão dos resultados, menor número de valor observado, geralmente, implica em menor número de pessoas envolvidas na coleta e isso reduz erros

Tipos de Amostragem

Amostragem probabilística: todos os elementos da população tiveram uma probabilidade ou a chance conhecida e diferente de zero de pertencer à amostra.

Amostragem não probabilística: não conhecemos a probabilidade ou a chance de um elemento da população pertencer à amostra.

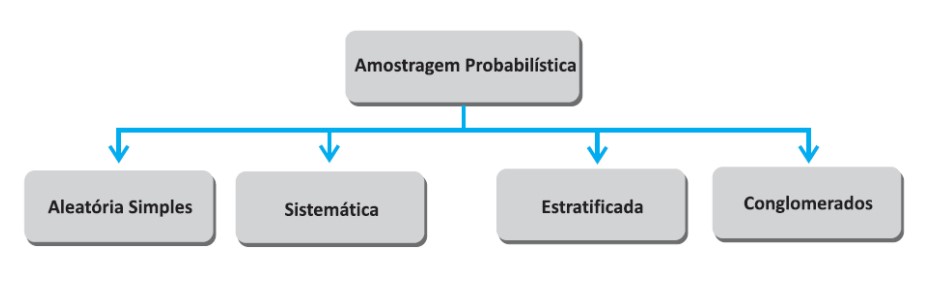
Amostragem Aleatória Simples (AAS)

A amostragem aleatória simples é uma das técnicas mais fundamentais e comuns de seleção de amostras em estatística. Ela envolve a escolha de uma amostra de uma população de forma aleatória, garantindo que cada indivíduo ou elemento da população tenha a mesma probabilidade de ser selecionado. Esse método é amplamente utilizado porque oferece uma abordagem objetiva e imparcial para a seleção de amostras, reduzindo a possibilidade de vieses e fornecendo resultados representativos da população.

Deve ser usada somente quando a população for homogênea em relação à variável que se deseja estudar. Pode se realizada por meio de um sorteio das unidades amostrais que compõe a população.

Vantagens:

Representatividade: Uma amostra aleatória simples tende a ser representativa da população, o que significa que as características da amostra devem refletir de forma precisa as características da população.

Imparcialidade: Todos os elementos têm a mesma probabilidade de serem selecionados, tornando o processo justo e livre de vieses.

Facilidade de Implementação: A amostragem aleatória simples pode ser relativamente fácil de implementar, especialmente com o uso de ferramentas estatísticas e tecnologia.

Generalização dos Resultados: Os resultados obtidos a partir da amostra aleatória simples podem ser generalizados para toda a população, desde que a amostra seja representativa e adequadamente selecionada.

Limitações:

Requer Lista de Elementos: Em algumas situações, pode ser difícil ou impossível obter uma lista completa de todos os elementos da população, o que dificulta a aplicação da amostragem aleatória simples.

Custos e Recursos: Em algumas pesquisas, o tamanho da população pode ser muito grande, exigindo uma amostra grande para garantir a representatividade. Isso pode ser custoso em termos de tempo, recursos e esforços de coleta de dados.

Amostragem Sistemática

A amostragem sistemática é uma técnica de seleção de amostras que envolve a escolha sistemática de elementos da população com um padrão regular. É uma abordagem mais simples e prática em comparação com a amostragem aleatória simples e pode ser útil quando a população é grande e não está organizada de forma aleatória.

Muitas vezes é possível obter uma amostra de características parecidas com a amostra aleatória simples, por um processo bem mais rápido. Por exemplo:

Tirar uma amostra de 1.000 fichas, dentre uma população de 5.000 fichas, pode-se tirar, sistematicamente, uma ficha a cada cinco (5.000/1.000 = 5).

Para garantir que cada ficha da população tenha a mesma probabilidade de pertencer à amostra, a primeira ficha deve ser sorteada, dentre as cinco primeiras.

Vantagens:

Facilidade de Implementação: A amostragem sistemática é relativamente fácil de implementar e requer menos esforços em comparação com a amostragem aleatória simples.

Eficiência: Pode ser mais eficiente do que a amostragem aleatória simples, especialmente quando a população está organizada de alguma forma.

Redução do Viés: Se a população exibir algum padrão regular, a amostragem sistemática pode ajudar a reduzir o viés associado à seleção aleatória, tornando-a uma opção viável em algumas situações.

Limitações:

Pode ser Tendenciosa: Se houver um padrão regular não aleatório na população, a amostragem sistemática pode introduzir viés na seleção, resultando em uma amostra que não é representativa da população.

Requer População Ordenada: A amostragem sistemática pressupõe que a população esteja ordenada de alguma forma, o que nem sempre é o caso em todas as situações.

Risco de Viés de Seleção: Se o padrão regular na população estiver relacionado à característica que está sendo estudada, pode haver um risco de viés de seleção.

Amostragem Estratificada

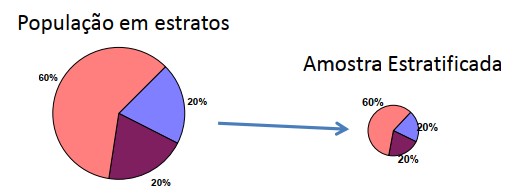
A amostragem estratificada é uma técnica de seleção de amostras que envolve a divisão da população em subgrupos homogêneos, chamados de estratos, seguidos pela seleção aleatória de amostras de cada estrato. Essa abordagem é útil quando a população possui características ou subgrupos distintos que podem afetar os resultados da pesquisa ou estudo. A amostragem estratificada visa garantir que cada estrato esteja adequadamente representado na amostra, permitindo inferências precisas e mais confiáveis sobre toda a população.

Em um caso particular de amostragem estratificada, a proporcionalidade do tamanho de cada estrato da população é mantida na amostra. Por exemplo, se um estrato corresponde a 20% do tamanho da população ele também deve corresponder a 20% da amostra.

Vantagens:

Representatividade Melhorada: A amostragem estratificada permite que cada estrato da população seja adequadamente representado na amostra, tornando as estimativas mais precisas e representativas da população como um todo.

Eficiência: Em alguns casos, a amostragem estratificada pode ser mais eficiente do que outros métodos de amostragem, pois pode reduzir o tamanho da amostra necessário para obter estimativas precisas.

Estudo de Subgrupos: Essa abordagem é particularmente útil quando há interesse em estudar subgrupos específicos da população, pois permite obter estimativas mais precisas para esses subgrupos.

Limitações:

Complexidade: A amostragem estratificada pode ser mais complexa do que outros métodos de amostragem, especialmente quando a população possui muitos estratos diferentes.

Dificuldade na Definição de Estratos: A definição adequada dos estratos é fundamental para o sucesso da amostragem estratificada, e isso pode ser desafiador em algumas situações.

Custos: Dependendo do número de estratos e do tamanho da população, a amostragem estratificada pode ser mais cara e exigir mais recursos do que outros métodos de amostragem.

Amostragem por Conglomerados

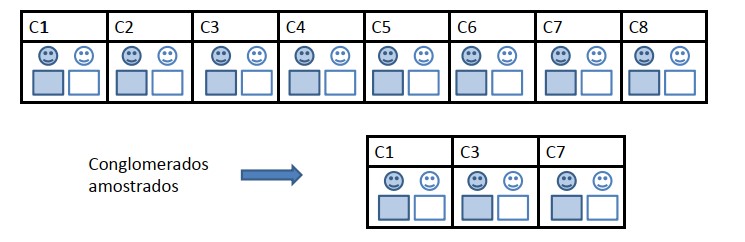
A amostragem por conglomerados é uma técnica de seleção de amostras que envolve a divisão da população em grupos ou conglomerados, seguida pela seleção aleatória de alguns desses conglomerados para compor a amostra. Ao contrário da amostragem estratificada, onde a divisão é feita em subgrupos homogêneos, na amostragem por conglomerados, os conglomerados podem ser heterogêneos em relação às características da população.

A população é dividida em conglomerados (grupos), sendo cada conglomerado representativo da população. Selecionamos aleatoriamente uma amostra de n conglomerados e a amostra é constituída por todos os elementos dos conglomerados selecionados.

Vantagens:

Redução do Custo e Tempo: A amostragem por conglomerados pode ser mais econômica e rápida em comparação com a amostragem aleatória simples ou estratificada, especialmente quando a população é grande e dispersa geograficamente.

Viabilidade Prática: Em algumas situações, é mais viável e conveniente agrupar a população em conglomerados e selecionar alguns deles aleatoriamente, em vez de tentar selecionar elementos individuais aleatoriamente.

Limitações:

Menor Precisão: A amostragem por conglomerados pode resultar em uma menor precisão das estimativas, uma vez que a variação dentro dos conglomerados pode ser maior do que a variação entre os conglomerados.

Risco de Viés: Se os conglomerados selecionados não forem representativos da população como um todo, pode ocorrer um viés de seleção, afetando a validade dos resultados.

Complexidade do Plano Amostral: A seleção de conglomerados requer um planejamento cuidadoso para garantir que a amostra seja representativa e que a precisão das estimativas seja adequada.

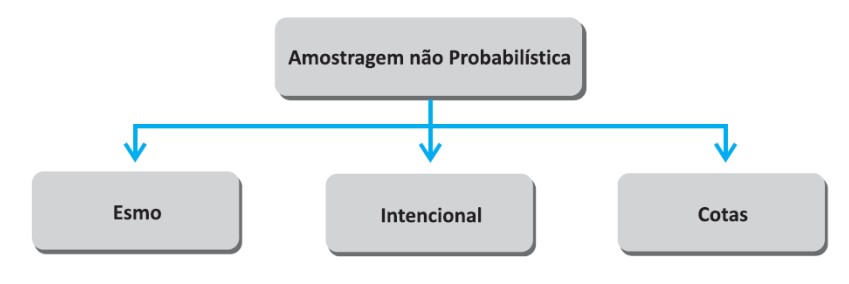
Amostragem a Esmo, Intencional ou por Cotas

A amostragem a Esmo, Intencional ou por Cotas é uma técnica de seleção de amostras que envolve a escolha deliberada e não aleatória dos elementos da população com base em critérios específicos. Nessa abordagem, o pesquisador seleciona propositadamente os indivíduos ou elementos que fazem parte da amostra, em vez de usar um método aleatório para a seleção. Essa técnica pode ser útil em algumas situações, mas é importante estar ciente de suas limitações e potenciais viéses.

Vantagens:

Facilidade de Implementação: A amostragem a Esmo, Intencional ou por Cotas pode ser mais fácil e rápida de implementar em comparação com métodos de amostragem aleatória, especialmente quando o pesquisador possui conhecimento prévio sobre a população e os critérios de seleção.

Seleção de Grupos Específicos: Essa técnica permite ao pesquisador selecionar propositadamente grupos específicos da população que são de interesse para o estudo ou pesquisa.

Limitações:

Viés de Seleção: A amostragem a Esmo, Intencional ou por Cotas pode introduzir viés de seleção, pois os elementos são escolhidos não aleatoriamente, o que pode afetar a representatividade e validade dos resultados.

Dificuldade de Generalização: Devido à seleção não aleatória, os resultados obtidos a partir da amostra podem não ser generalizáveis para a população como um todo.

Subjetividade: A escolha dos elementos da amostra é subjetiva e depende do julgamento do pesquisador, o que pode comprometer a objetividade do estudo.

Dificuldade de Estimação da Precisão: É mais difícil estimar a precisão das estimativas obtidas a partir de uma amostra por Esmo, Intencional ou por Cotas, pois não há uma base estatística para calcular a margem de erro.

Cálculo do tamanho da amostra

Considerando que seus dados seguem uma distribuição normal, utilize o seguinte site para realizar o cálculo do tamanho da sua amostra:

https://pt.surveymonkey.com/mp/sample-size-calculator/

Cálculo da margem de erro

Também considerando que seus dados seguem uma distribuição normal e você queira saber qual a margem de erro baseado na quantidade de registros de sua amostra, use o seguinte site para o cálculo:

https://pt.surveymonkey.com/mp/margin-of-error-calculator/

Medidas de Posição

As medidas de posição, também conhecidas como medidas de tendência central, são estatísticas utilizadas para resumir e descrever a distribuição de um conjunto de dados. Elas representam valores centrais que indicam onde a maioria dos dados se concentra ou se agrupa.

Os quartis e percentis são medidas estatísticas que dividem um conjunto de dados ordenados em partes iguais ou proporcionais. Eles são utilizados para avaliar a distribuição e a dispersão dos dados, bem como para identificar valores específicos que representam posições relativas dentro da distribuição.

Quartis

Os quartis dividem os dados ordenados em quatro partes iguais, representando os valores que separam o conjunto de dados em quartos. O primeiro quartil (Q1) é o valor que separa os 25% menores dos dados, o segundo quartil (Q2) é a mediana, que separa os 50% menores dos dados dos 50% maiores, e o terceiro quartil (Q3) separa os 25% maiores dos dados.

Se o conjunto de dados tiver um número ímpar de elementos, o cálculo da mediana é simples, pois ela é exatamente o valor central. No entanto, se o número de elementos for par, a mediana é a média dos dois valores centrais. Os quartis são especialmente úteis quando se deseja avaliar a dispersão dos dados e identificar possíveis valores atípicos ou outliers.

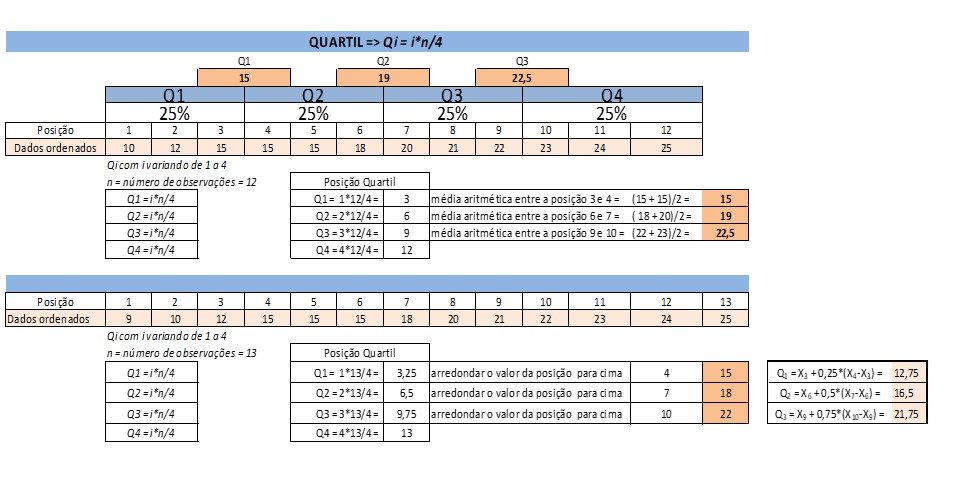
A partir da posição, pode-se calcular o valor do quartil. Como regra geral, se a posição coincide com um número inteiro, o valor a ser usado é o da média aritimética entre os dados que ocupam as posições i e i + 1. Se a posição não for um número inteiro, a convenção que iremos usar é arrendondar para a posição do número acima da posição e tomar o valor correspondente.

Percentis

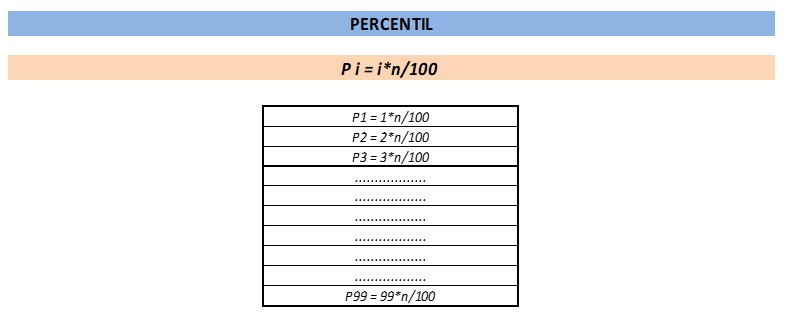
Os percentis são semelhantes aos quartis, mas dividem os dados em 100 partes iguais ou percentuais. O p-ésimo percentil é o valor que separa p% dos dados do restante. O percentil mais conhecido é o percentil 50, que é exatamente a mediana, separando os 50% menores dos dados dos 50% maiores.

Outros percentis também são frequentemente usados, como o percentil 25 (Q1) e o percentil 75 (Q3), que correspondem aos quartis mencionados anteriormente. Além disso, o percentil 1 (P1) é o valor que separa os 1% menores dos dados, o percentil 99 (P99) é o valor que separa os 99% menores dos dados e assim por diante.

Os percentis são especialmente úteis para identificar a posição relativa de um valor em um conjunto de dados. Por exemplo, o percentil 90 indica que 90% dos dados são menores do que esse valor e 10% são maiores.

Exercício 1: Dado o conjunto de dados abaixo, calcule o valor do Q1, Q2, Q3, P10 e P90:

10, 12, 15, 18, 20, 22, 25, 28, 30, 35, 40, 45, 50

a) Q1 = 10, Q2 = 18, Q3 = 25, P10 = 12 e P90 = 50

b) Q1 = 12, Q2 = 18, Q3 = 30, P10 = 10 e P90 = 45

c) Q1 = 12, Q2 = 20, Q3 = 35, P10 = 12 e P90 = 40

d) Q1 = 15, Q2 = 18, Q3 = 30, P10 = 10 e P90 = 35

e) Q1 = 18, Q2 = 25, Q3 = 35, P10 = 12 e P90 = 45

Medidas de Forma

As medidas de forma, também conhecidas como medidas de assimetria e curtose, são estatísticas utilizadas para descrever a forma da distribuição de um conjunto de dados. Essas medidas complementam as medidas de tendência central (média, mediana e moda) e ajudam a entender como os dados estão distribuídos em torno dessas medidas centrais.

Existem duas principais medidas de forma:

Assimetria

A assimetria mede o grau de desvio da distribuição em relação à simetria. Uma distribuição é considerada simétrica quando a metade esquerda é uma imagem espelhada da metade direita em relação à medida de tendência central (média, mediana ou moda). Se a distribuição for simétrica, a assimetria é zero.

Assimetria positiva: Quando a cauda direita da distribuição é mais longa ou estendida em relação à cauda esquerda. Nesse caso, a média é maior que a mediana e a moda.

Assimetria negativa: Quando a cauda esquerda da distribuição é mais longa ou estendida em relação à cauda direita. Nesse caso, a média é menor que a mediana e a moda.

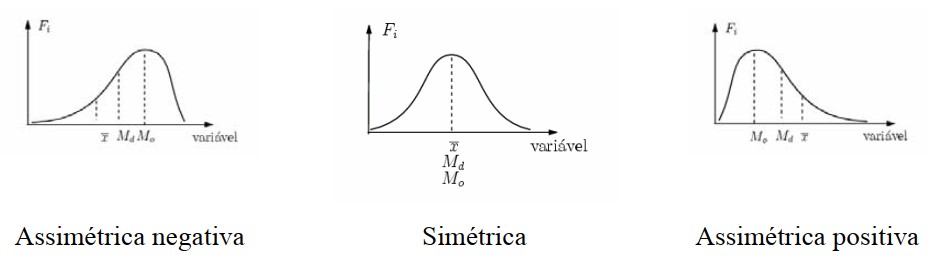
A medida mais comumente utilizada para calcular a assimetria é o coeficiente de assimetria de Pearson (AS), também conhecido como coeficiente de Pearson ou simplesmente coeficiente de assimetria.

Onde:

x̄: média aritimética

Mo: moda

s: desvio-padrão

Md: mediana

Curtose

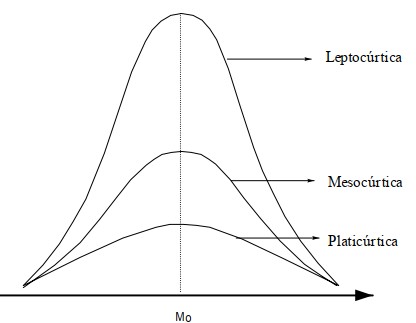
A curtose (K) mede o grau de achatamento ou agudez da distribuição em relação a uma distribuição normal. Uma distribuição normal tem curtose K = 0,263 (mesocúrtica), e qualquer valor diferente disso indica uma distribuição mais ou menos achatada em relação à normal.

Curtose K < 0,263 (curtose leptocúrtica): A distribuição é mais afunilada e concentrada no centro em relação à normal. Tem caudas mais pesadas e um pico mais alto.

Curtose K > 0,263 (curtose platicúrtica): A distribuição é mais achatada e dispersa em relação à normal. Tem caudas menos pesadas e um pico mais suave.

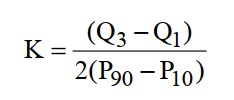
Gráficos Avançados

Gráficos avançados são representações visuais mais complexas e detalhadas de dados que vão além dos gráficos básicos, como gráficos de barras, gráficos de linhas e gráficos de pizza. Eles são usados para visualizar informações mais específicas, multidimensionais ou complexas, proporcionando uma maneira poderosa de explorar e comunicar padrões, tendências e relações entre variáveis nos dados.

Diagrama ramo e folhas

O diagrama Ramo-e-Folhas, criado por John Tukey, é um procedimento utilizado para armazenar os dados sem perda de informação. É utilizado para se ter uma idéia visual da distribuição dos dados. Cada valor observado, xi, da variável X, deve consistir de no mínimo dois dígitos e a variável pode ser tanto quantitativa discreta como contínua.

Para construí-lo, divide-se cada número em duas partes. A primeira é denominada ramo e a segunda, folhas. O ramo consistirá de um ou mais dígitos iniciais se o valor da variável for um número inteiro e do número inteiro, se o valor da variável for um número com decimais. Nas folhas, colocam-se os dígitos restantes se o valor observado for número inteiro, ou os decimais, caso contrário.

Dado o seguinte conjunto de dados, construa o diagrama de ramos e folhas para a idade dos respondentes:

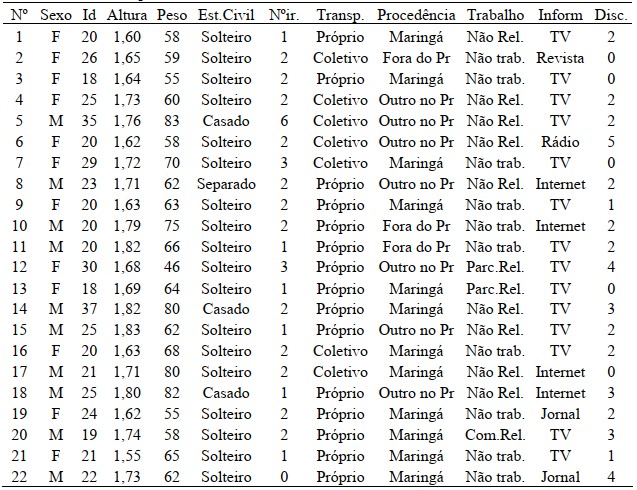
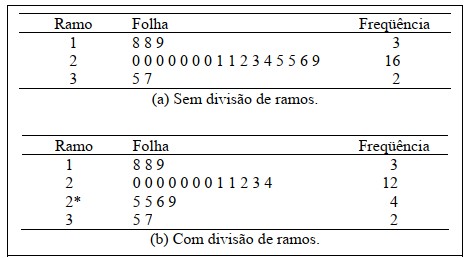
Observa-se que o ramo correspondente ao dígito 2 tem muitas folhas. Neste caso, a opção é dividir este ramo em dois: as folhas de 0 a 4 pertencerão a uma linha e as folhas de 5 a 9 pertencerão à outra linha. Os ramos são discriminados por um sinal no seu expoente (*).

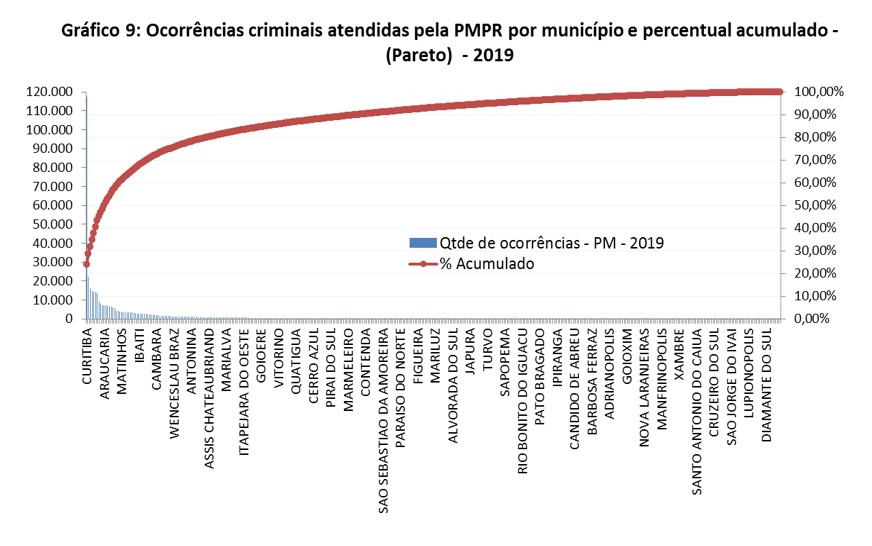
Gráfico de Pareto

O gráfico de Pareto é uma ferramenta de visualização que combina um gráfico de barras com um gráfico de linha e é usado para destacar a importância relativa dos diferentes elementos em um conjunto de dados. Esse tipo de gráfico é útil quando se deseja identificar quais elementos têm maior impacto ou contribuição para um determinado resultado, permitindo uma alocação mais eficiente de recursos e esforços.

O gráfico de Pareto é baseado no Princípio de Pareto, também conhecido como a regra 80/20, que sugere que, em muitos cenários, aproximadamente 80% dos efeitos são causados por 20% das causas. Esse princípio é aplicável a diversas situações, como em economia, gestão de qualidade, gerenciamento de projetos, entre outros.

Construção do gráfico de Pareto:

1. Identificar a categoria e a frequência: Primeiro, identifique as categorias ou elementos a serem analisados e conte a frequência ou ocorrência de cada categoria no conjunto de dados.

2. Ordenar as categorias: Ordene as categorias em ordem decrescente com base em suas frequências, da maior para a menor.

3. Calcular as frequências acumuladas: Calcule as frequências acumuladas somando as frequências de cada categoria até a categoria atual. Isso mostra a contribuição cumulativa de cada categoria para o total.

4. Construir o gráfico: Crie um gráfico de barras para representar a frequência de cada categoria e um gráfico de linha para representar as frequências acumuladas. As barras são dispostas em ordem decrescente e a linha mostra a evolução das frequências acumuladas.

Boxplot

O gráfico Box Plot (ou desenho esquemático) é uma análise gráfica que utiliza cinco medidas estatísticas: valor mínimo, valor máximo, mediana, primeiro e terceiro quartil da variável quantitativa. Este conjunto de medidas oferece a idéia da posição, dispersão, assimetria, caudas e dados discrepantes. A posição central é dada pela mediana e a dispersão pelo desvio interquartílico IQ (ou dj) = Q3 - Q1. As posições relativas de Q1 , Q2 e Q3 dão uma noção da assimetria da distribuição. Os comprimentos das caudas são dados pelas linhas que vão do retângulo aos valores atípicos.

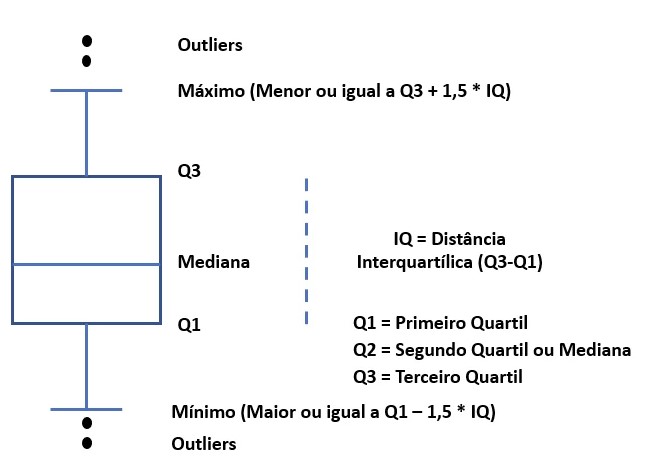
Considerando os seguintes dados de idades:

18 18 19 20 20 20 20 20 20 21 21

22 23 24 25 25 25 26 29 30 35 37

Temos as seguintes medidas necessárias para a construção do boxplot:

Mediana: 21,5

Q1: 20

Q3: 25

IQ = Q3 - Q1: 5

Limite inferior: Q1 - 1,5*IQ: 12,5

Limite superior: Q3 + 1,5*IQ: 32,5

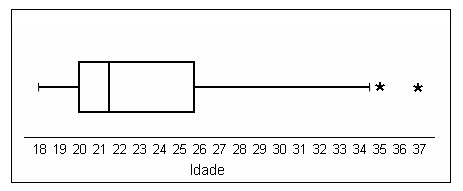
No conjunto de dados não existe aluno com idade inferior a 12,5, ou seja, não há aluno com idade considerada discrepante inferiormente. Entretanto, existem dois indivíduos cujas idades são superiores a 32,5, pontos estes considerados discrepantes (outliers) neste conjunto de dados: as idades 35 e 37. Estes pontos são identificados no boxplot por meio de um asterisco na direção das linhas traçadas.

Note-se que no intervalo interquartílico (dentro do retângulo) existem 50% dos dados, dos quais, 25% estão entre a linha da mediana e a linha do primeiro quartil e os outros 25% estão entre a linha da mediana e a linha do terceiro quartil. Cada linha da cauda mais os valores discrepantes contêm os 25% restantes da distribuição. A Figura acima mostra que a distribuição das idades dos alunos apresenta assimetria positiva, ou seja, dispersam-se para os valores maiores.

Exercício 2: Dado o seguinte conjunto de valores:

65, 78, 82, 90, 94, 75, 85, 72, 68, 88, 80, 98, 91, 84, 77, 89

a) Construa o gráfico de boxplot para os dados apresentados.

b) Existe algum valor discrepante no conjunto de dados?

c) O que se pode considerar em relação à apresentação dos dados?