Módulo 1

Introdução à Estatística

A estatística é uma disciplina que envolve a coleta, análise, interpretação, apresentação e organização de dados. Ela nos ajuda a entender e descrever fenômenos complexos do mundo real através de números e dados. De experimentos científicos a pesquisas de opinião, de estudos de saúde a análises de mercado, a estatística desempenha um papel crucial em muitos campos. Existem dois grandes ramos da estatística: a estatística descritiva e a estatística inferencial; além do cálculo de probabilidades.

Estatística Descritiva: Este ramo da estatística envolve a organização e a sumarização de dados. Quando recebemos um conjunto grande de dados, é impraticável e muitas vezes inútil analisá-los sem qualquer estrutura ou sumarização. A estatística descritiva nos ajuda a resumir esses dados de uma maneira que seja fácil de entender. Isso pode ser feito através de tabelas, gráficos, e medidas de tendência central (como a média, a mediana e a moda) e medidas de dispersão (como a variância e o desvio padrão).

Estatística Inferencial: Este ramo da estatística nos permite fazer inferências ou previsões sobre uma população com base em dados de uma amostra dessa população. Em muitos cenários, é impraticável ou impossível medir todos os membros de uma população. Assim, selecionamos uma amostra da população e fazemos inferências sobre a população inteira com base nesses dados da amostra. Para isso, a estatística inferencial usa técnicas como testes de hipóteses, correlação e regressão.

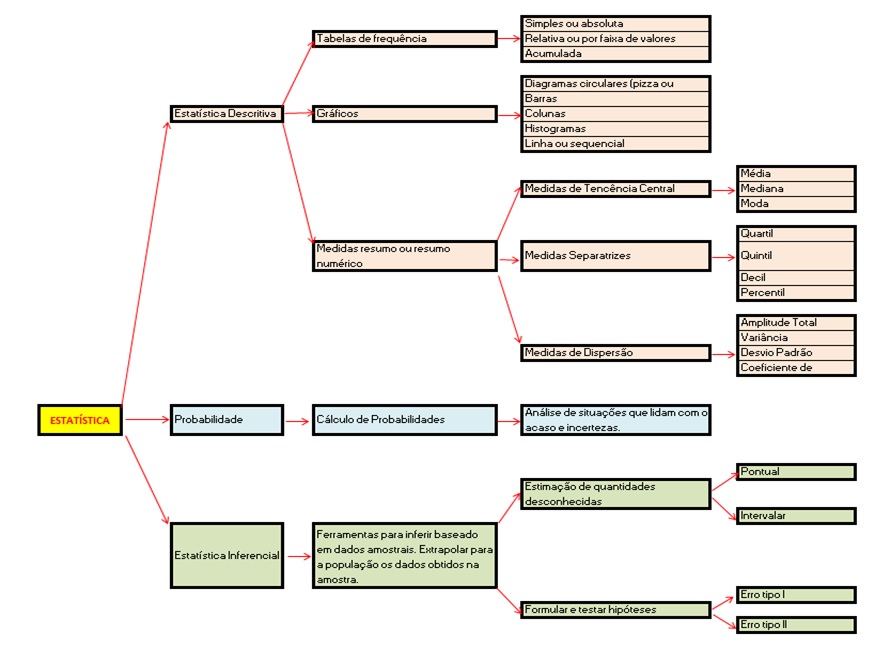
Na estatística, os parâmetros são medidas numéricas que descrevem características de uma população, enquanto as estatísticas são medidas numéricas que descrevem características de uma amostra. A diferença entre parâmetros e estatísticas é crucial para entender muitos conceitos em estatística.

Importância da estatística

A estatística é uma disciplina crucial por diversas razões:

1. Tomada de Decisão: A estatística oferece ferramentas para tomar decisões informadas em situações de incerteza. Em ambientes de negócios, por exemplo, a estatística é usada para analisar tendências de mercado, prever demanda e otimizar operações.

2. Pesquisa: A estatística é fundamental para a condução de pesquisas em uma ampla variedade de campos, como medicina, psicologia, educação e ciências sociais. Testes de hipóteses, projetos experimentais e análise de regressão são apenas algumas das ferramentas estatísticas que permitem aos pesquisadores tirar conclusões a partir de seus dados.

3. Governo e Política: No setor público, a estatística é usada para formular políticas e programas baseados em evidências. Estatísticas populacionais, econômicas e de saúde informam sobre a alocação de recursos, a implementação de políticas e a avaliação de programas.

4. Qualidade e Melhoria de Processos: No campo da qualidade e melhoria de processos, técnicas estatísticas são usadas para monitorar e melhorar a qualidade da produção e dos processos operacionais.

5. Compreensão do Mundo: A estatística nos ajuda a entender padrões e tendências no mundo ao nosso redor. Ela nos permite entender padrões em dados, como tendências climáticas, padrões de comportamento humano e desenvolvimentos econômicos.

Coleta e Apresentação dos Dados

A coleta de dados é uma parte essencial da estatística e envolve o processo de reunir informações relevantes para responder uma pergunta de pesquisa, testar uma hipótese ou avaliar uma teoria. É o primeiro passo na análise de dados e é realizado através de várias técnicas, incluindo:

1. Pesquisas ou questionários: A pesquisa é uma técnica de coleta de dados que envolve a obtenção de informações diretamente de indivíduos. Isso pode ser feito através de entrevistas, questionários ou pesquisas online.

2. Observação: A observação é uma técnica de coleta de dados que envolve a obtenção de informações através da observação de indivíduos ou eventos. Isso pode ser feito através de observação direta ou observação participante.

3. Experimentação: A experimentação é uma técnica de coleta de dados que envolve a manipulação de variáveis para testar hipóteses e avaliar relações de causa e efeito. Isso pode ser feito através de experimentos controlados ou experimentos naturais.

4. Análise de registros existentes: Revisar dados que já foram coletados e registrados, como dados demográficos, registros médicos ou resultados de testes.

Apresentação dos Dados

A apresentação de dados é o processo de organizar e visualizar dados de uma forma que torne a informação clara e fácil de entender. A apresentação eficaz dos dados ajuda a comunicar os resultados de uma forma que seja significativa para os outros. As técnicas comuns de apresentação de dados incluem:

1. Tabelas e gráficos: As tabelas permitem apresentar dados brutos e resumidos de uma forma clara e concisa, enquanto os gráficos permitem visualizar padrões e tendências nos dados.

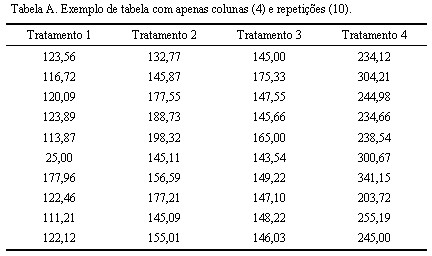
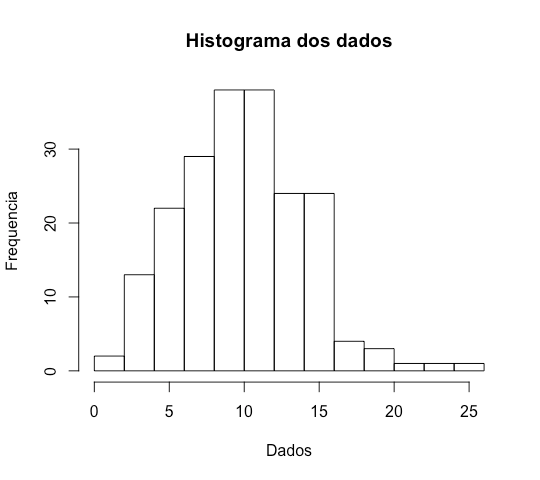
2. Diagramas: Diagramas como diagramas de caixa, histogramas, diagramas de barras e diagramas de pizza podem ser usados para representar diferentes aspectos dos dados.

3. Mapas: Os mapas são úteis para apresentar dados geográficos ou espaciais.

4. Infográficos: Infográficos são representações visuais de informações que usam elementos de design para apresentar dados de uma forma atraente e fácil de entender.

População e Amostra

Na estatística, a população refere-se ao conjunto completo de indivíduos, itens ou eventos que se deseja estudar. A população pode ser definida de diversas maneiras, dependendo do objetivo do estudo. Por exemplo, a população pode ser todos os habitantes de um país, todos os alunos de uma escola, todas as transações de vendas em uma loja durante um ano, ou todos os pacientes que têm uma determinada doença.

O conceito de população é fundamental para a inferência estatística, que é o processo de tirar conclusões sobre uma população com base em uma amostra dessa população.

Uma amostra é um subconjunto da população que é selecionado para participar de um estudo. Em muitos casos, seria muito difícil, caro ou mesmo impossível coletar dados de todos os membros de uma população. Portanto, os pesquisadores selecionam uma amostra da população que eles acreditam ser representativa da população como um todo.

A amostra deve ser selecionada de forma a refletir as características da população de interesse. Se a amostra for representativa, os pesquisadores podem fazer generalizações sobre a população com base nos dados da amostra.

Há várias maneiras de selecionar uma amostra de uma população, e a escolha do método de amostragem pode ter um impacto significativo sobre os resultados do estudo. Métodos comuns de amostragem incluem amostragem aleatória simples, amostragem estratificada e amostragem por conglomerados, entre outros.

É importante notar que, mesmo com uma amostragem cuidadosa, há sempre algum grau de incerteza ao fazer inferências sobre a população com base em uma amostra. Esta incerteza é muitas vezes expressa em termos de erro de amostragem e intervalos de confiança.

Fases do Método Estatístico

-Definição do problema;

-Planejamento da pesquisa;

-Coleta de dados;

-Organização e tratamento dos dados;

-Análise e interpretação dos resultados;

-Apresentação dos resultados (conclusões).

Estatística Descritiva

A estatística descritiva é um ramo da estatística que lida com a apresentação e descrição de conjuntos de dados. Ela fornece resumos sobre a amostra e as medidas que foram feitas. Em outras palavras, é sobre a descrição, listagem, ou a sumarização dos dados de maneira conveniente e informativa.

A estatística descritiva pode ser dividida em duas categorias:

1. Medidas de tendência central: São medidas que indicam onde o centro de um conjunto de dados está localizado. Essas incluem a média (ou média aritmética), que é a soma de todos os valores dividida pelo número de valores; a mediana, que é o valor do meio de um conjunto de dados ordenado; e a moda, que é o valor mais frequente em um conjunto de dados.

2. Medidas de dispersão: São medidas que indicam o quão espalhados os dados estão, ou o quão longe eles estão do centro. Estas incluem a variância e o desvio padrão, que são medidas de variação que mostram o quão distante, em média, os valores estão da média; o alcance, que é a diferença entre o maior e o menor valor em um conjunto de dados; e o desvio absoluto médio, que é a média das diferenças absolutas entre cada valor e a média.

Classificação de variáveis

Em estatística, uma variável é qualquer característica ou atributo que pode ser medido ou observado e que pode assumir diferentes valores. As variáveis são classificadas em diferentes tipos, com base nas características e nos valores que elas podem assumir. A classificação das variáveis é crucial para determinar o tipo de análise estatística que pode ser realizada em um conjunto de dados. As variáveis geralmente são classificadas em dois tipos principais: variáveis qualitativas e variáveis quantitativas.

Variáveis Qualitativas: Também conhecidas como variáveis categóricas, as variáveis qualitativas são variáveis que descrevem uma característica ou atributo. Elas podem ser classificadas em dois tipos: variáveis nominais e variáveis ordinais.

-Variáveis Nominais: As variáveis nominais são variáveis que não têm uma ordem natural. Elas são usadas para identificar ou categorizar. Por exemplo, o sexo de uma pessoa (masculino ou feminino) é uma variável nominal, pois não há uma ordem natural entre os dois valores. Outros exemplos de variáveis nominais incluem cor dos olhos, cor do cabelo, estado civil, país de origem, CEP, número do CPF, etc.

-Variáveis Ordinais: As variáveis ordinais são variáveis que têm uma ordem natural. Elas são usadas para identificar ou categorizar, assim como as variáveis nominais, mas também podem ser ordenadas ou classificadas. Por exemplo, o nível de educação de uma pessoa (ensino fundamental, ensino médio, ensino superior) é uma variável ordinal, pois há uma ordem natural entre os três valores. Outros exemplos de variáveis ordinais incluem nível de satisfação (muito insatisfeito, insatisfeito, neutro, satisfeito, muito satisfeito), nível de dor (nenhuma dor, dor leve, dor moderada, dor severa), etc.

Variáveis Quantitativas: As variáveis quantitativas são variáveis que podem ser medidas ou contadas. Elas podem ser classificadas em dois tipos: variáveis discretas e variáveis contínuas.

-Variáveis Discretas: As variáveis discretas são variáveis que assumem valores inteiros. Elas são usadas para contar. Por exemplo, o número de filhos de uma pessoa é uma variável discreta, pois só pode assumir valores inteiros (1 filho, 2 filhos, 3 filhos, etc.). Outros exemplos de variáveis discretas incluem número de alunos em uma sala de aula, número de carros em um estacionamento, número de pessoas em uma fila, etc.

-Variáveis Contínuas: As variáveis contínuas são variáveis que podem assumir qualquer valor dentro de um intervalo contínuo. Elas são usadas para medir. Por exemplo, a altura de uma pessoa é uma variável contínua, pois pode assumir qualquer valor dentro de um intervalo contínuo (1,50 m, 1,51 m, 1,52 m, etc.). Outros exemplos de variáveis contínuas incluem peso, temperatura, pressão arterial, etc.

Exercício 1: Classifique as variáveis abaixo em qualitativas ou quantitativas, e em nominais, ordinais, discretas ou contínuas:

a) Idade:

b) Classe sócio econômica:

c) Diagnóstico de um doente:

d) Grupo sanguíneo:

e) Índice de massa corporal:

f) Grau de concordância (discordo totalmente, discordo, concordo, concordo totalmente):

Medidas de tendência central

As medidas de tendência central procuram descrever, através de uma estatística (estimativa pontual) um valor médio (típico ou padrão).

Média: A média é a soma de todos os valores dividida pelo número de valores. Ela é calculada somando todos os valores e dividindo o resultado pelo número de valores. A média é a medida de tendência central mais comumente usada. Ela é usada para descrever conjuntos de dados simétricos, sem valores extremos. A média é representada pela letra grega μ (mi) e x barra (x̄) para a média amostral.

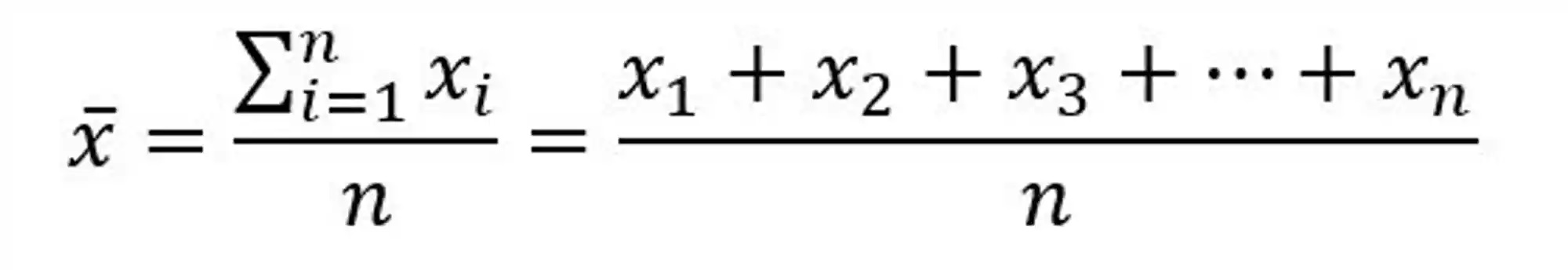
Mediana: A mediana é o valor do meio de um conjunto de dados ordenado. Ela é calculada ordenando todos os valores e localizando o valor do meio. Se o número de valores for ímpar, o valor do meio é a mediana. Se o número de valores for par, a mediana é a média dos dois valores do meio. A mediana é usada para descrever conjuntos de dados assimétricos, com valores extremos. A mediana é representada pela letra grega M (maiúsculo).

Moda: A moda é o valor que ocorre com mais frequência em um conjunto de dados. Ela é calculada contando o número de vezes que cada valor ocorre e determinando qual valor ocorre com mais frequência. A moda é usada para descrever conjuntos de dados simétricos ou assimétricos, com ou sem valores extremos. A moda é representada pela letra grega Mo (maiúsculo).

Exercício 2: Foram coletados sete valores de salário dos trabalhadores da construção civil: 300,00; 460,00; 200,00; 510,00; 250;00; 450,00; 250,00. Calcule a média, a mediana e a moda. O que você pode informar a respeito dos valores? Se tivéssemos incluído nesta análise o salário do engenheiro (2300,00), quais seriam os resultados e as informações que você tiraria a respeito?

Exercício 3: Consideremos agora uma amostra de dados bancários. Os valores relacionados são tempo de espera (em minutos) de clientes.

Banco A: 6,5 - 6,6 - 6,7 - 6,8 - 7,1 - 7,3 - 7,4 - 7,7 - 7,7 - 7,7 (fila única)

Banco B: 4,2 - 5,4 - 5,8 - 6,2 - 6,7 - 7,7 - 7,7 - 8,5 - 9,3 - 10,0 (fila múltipla)

Calcule a média, a mediana e a moda. O que você pode informar a respeito dos valores? Qual banco você escolheria para ser atendido?

Medidas de dispersão

As medidas de dispersão procuram descrever a variabilidade dos dados em torno de uma medida de tendência central.

Amplitude: A amplitude é a diferença entre o maior e o menor valor de um conjunto de dados. Ela é calculada subtraindo o maior valor do menor valor. A amplitude é usada para descrever conjuntos de dados simétricos ou assimétricos, com ou sem valores extremos. A amplitude é representada pela letra AT (maiúsculo).

Variância: A variância é a média dos quadrados dos desvios em relação à média. Ela é calculada subtraindo-se cada valor da média, elevando o resultado ao quadrado, somando os resultados e dividindo-se o total pelo número de valores (menos um, no caso da variância amostral). A variância é usada para descrever conjuntos de dados simétricos, sem valores extremos. A variância é representada pela letra grega σ2 (sigma ao quadrado) e s2 (minúsculo).

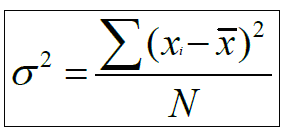
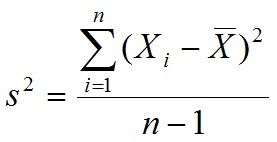
Desvio padrão: O desvio padrão é a medida de dispersão mais comumente usada. Ele é calculado subtraindo-se cada valor da média, elevando-se o resultado ao quadrado, somando-se os resultados e dividindo-se o total pelo número de valores (menos um, no caso do desvio amostral) e tirando-se a raiz quadrada do resultado. O desvio padrão é usado para descrever conjuntos de dados simétricos, sem valores extremos. O desvio padrão é representado pela letra grega σ (sigma) e s (minúsculo para a amostra).

Consideremos os seguintes conjuntos:

A = {5,5,5,5,5}

B = {3,4,5,6,7}

C = {13,14,15,16,17}

D = {1,3,5,7,9}

E = {3,5,5,5,7}

F = {3,3,4,4,5,5,6,6,7,7}

A média aritimética dos elementos do conjunto C é 15, e para todos os demais conjuntos a média dos seus elementos é 5.

Com base no simples exame desses conjuntos, podemos fazer as seguintes afirmativas, relativas à dispersão dos valores dos elementos de cada conjunto:

1) o conjunto A apresenta dispersão nula;

2) os conjuntos B e C apresentam a mesma dispersão, só diferindo quanto à média;

3) a dispersão de D é maior do que a dispersão de B; ainda, como para o conjunto D a diferença entre dois valores consecutivos é sempre igual a 2 e para o conjunto B é sempre igual a 1, pode-se afirmar que a dispersão de D é o dobro da dispersão de B;

4) a dispersão de E é maior do que a dispersão de A, mas menor do que a dispersão de B;

5) o conjunto F apresenta dispersão igual à de B, pois esses conjuntos só diferem quanto ao número de elementos (o conjunto F é uma duplicação de B).

Exercício 4: Assinale como verdadeiro ou falso:

a) [ ] Em um conjunto de valores, todos iguais, o desvio-padrão também é igual à constante.

b) [ ] Na série 60, 50, 90, 70 e 80, o valor 70 será a média e a mediana.

c) [ ] A média aritmética é a razão entre o somatório dos valores e o número deles.

d) [ ] A medida que tem o mesmo número de valores abaixo e acima dela é a mediana.

Exercício 5: Em um seminário de sociologia, seis estudantes foram testados por meio de um instrumento que produz mensurações de nível intervalar. O objetivo da pesquisa era mensurar suas atitudes com relação a um grupo minoritário. Suas respostas, numa escala de 1 a 10 (quanto mais alto o escore, mais favorável a atitude), foram: 5, 2, 6, 3, 1 e 1. Relativamente aos escores, calcule:

a) A moda.

b) A mediana.

c) A média.

d) A amplitude.

e) O desvio-padrão.

f) No geral, até que ponto esses estudantes são favoráveis ao grupo minoritário? Justifique sua resposta.

g) Identifique e classifique a variável deste problema.